Mathematical problem solving#
See also: teaching-mathematics
A collection of insights/perspectives on problem solving in mathematics - particularly related pedagogies.
There does appear to be a tendency for these problem solving models to be represented as sequential steps. i.e. mini waterfall methods where one step is completed before the next is started - the world (and what we do it it) isn't that sequential - see pedagogy-before-technology. A perspective which echoes with a comment Boaler makes about mathematicians doing a lot of "playing with mathematics" as they try to solve a problem.
Wolfram TED Talk (2010)#
Four stage process for working on mathematics
- Posing a question
- Going from the real world to a mathematical model
- Performing a calculation
- Going from the model back to the real world, to see if the original question was answered
Wolfram argues that 80% of school mathematics is spent on stage 3.
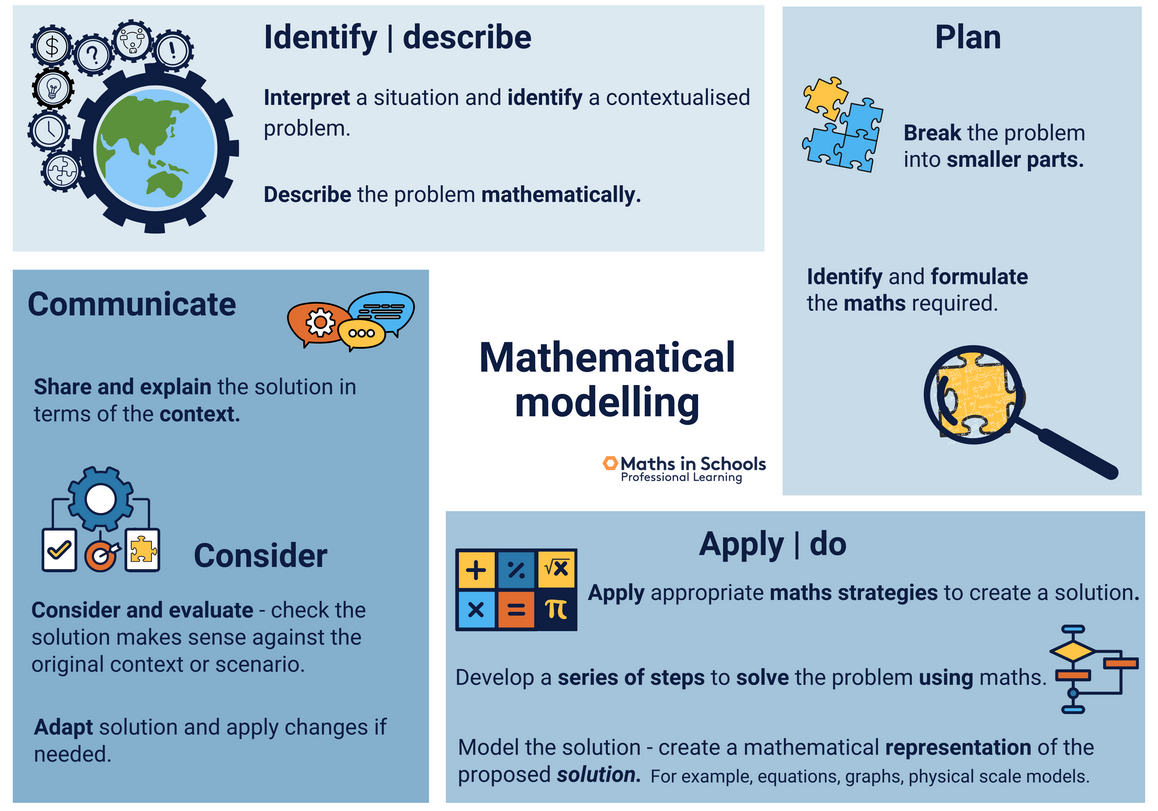
Australian curriculum maths-in-schools#
Offers the following diagram which aims to represent what the v9-oz-mathematics-learning-area offers as a mathematics modelling process using "mathematics to formulate, analyse, solve, interpret, generalise and communicate their results in response to a real-world situation"
The image offers the following process
-
Identify | describe
- Interpret a situation and identify a contextualised problem
- Describe the problem mathematically
-
PLan
- Break the problem into smaller parts
- Identify and formulate the maths required
-
Apply | do
- Apply appropriate maths strategies to create a solution.
- Develop a series of steps to solve the problem using maths.
- Model the solution - create a mathematical representation of the proposed solution
-
Communicate
- Share and explain the solution in terms of the context.
-
Consider
- Consider and evaluate - check the solution makes sense against the original context or scenario
- Adapt solution and apply changes if needed