Exploring australian curriculum#
See also: casa, datasette, australian-curriculum, other-oz-curriculum-code-projects, big-ideas-in-mathematics
Development log#
- 27 August 2023 - 001-exploring-oz-dev-log - initial import v8.4, datasette
- 24 September 2023 - 002-exploring-oz-dev-log - importing v9, links with memex
- 18 November 2023 - 003-exploring-oz-dev-log - Experiments with Neo4j - ended in failure due to Neo4J plugin difficulties
- 11 December 2023 - 004-exploring-oz-dev-log some slow glimmers with rdflib
-
25 December 2023 - 005-exploring-oz-dev-log - generating some markdown for memex - complete
To do#
- Further australian curriculum parsing
- Capabilities (esp. numeracy) to access the learning progression information
- Cross curriculum priorities
- content descriptions use the
dcterms:relationto link to other learning areas via URI e.g. (AC9M9ST01) - Can the maths glossary be converted from .docx to something useful?
- Explore views similar to that provided by this AMSI spreadsheet which illustrates some useful ways to represent just the curriculum - minimal linkages outside (e.g. big ideas)
What?#
The australian-curriculum defines most of what Australian school students learn. It is provided as website and related resources. For teachers, understanding and working with the curriculum is an essential part of their work. But no website can serve all the potential uses for the curriculum and its content. This casa serves a few purposes, including
- Explore how the Australian Curriculum can be made more generative.
- Offer a purposeful reason to explore different Python based technologies in service of that goal.
- Explore various useful applications of a generative Australian Curriculum to teachers and schools.
- Encourage me to explore and better understand the curriculum for my teaching areas - teaching-mathematics and teaching-digital-technologies
Current code is available in the project's Git repo
Early explorations of the the australian-curriculum. Taking a CSV download and using one or two Python data visualisation tools.
Related work#
Wikidata for Education a 2020 project started by Wikimedia foundation to mak curriculum data more open. Has produced a data model. This model document gives more detail. Initial project working Ghana's curriculum. -- related presentation
Links to related documents, including
- Ward & Nicholas (2010) - USQ based work pushing the semantic web approach and benefits to curriculum
- Barker (2020) - blog post on connected educational content and curriculum frameworks. It references a BBC Curriculum (that now 404s). Also mentions OER Schema
The Australian Curriculum - through the company implementing the curriculum site - has done a lot of work with RDF/semantic web/linked data. This 2010 interview is hosted on a company site that talks about the Schools Online Thesaurus (ScOT). Going into a lot of detail for the benefits of the approach (and the complexity). A pre-cursor to the Australian Curriculum in current form. In turn linked to Golder et al (2010)
What might some useful applications be?#
Slowly emerging from the sections below are the following "strands" that might be usefully woven together
-
Curriculum - big ideas used to bring related standards together and map out links with other big ideas.
Allowing connections to be made across a learning area and possibly beyond. The ALIVE approach includes linked as an important feature of good mathematics teaching and includes mention of the challenges arising from curriculum organisation - i.e. helping teacher see/remember these links will help with pedagogy.
Which appears linked to the idea of curriculum-ergonomics
-
(Cultural) Context - weaving in different contexts with whichever curriculum "unit" is the focus (big idea, standard etc)
Helping teachers weave in the context explicitly, but also through teaching approaches that enable student agency to do this weaving. Perhaps even requiring it? Roberts (2023b) cites Certeau (1980) as classifying this work as strategies and tactics? More broadly under the term curriculum enactment and integrated curriculum models?
Curriculum studies#
Roberts (2023b) emphasis added
To reference Pinar’s (2004, P.2) seminal text "what is curriculum theory?" curriculum theory "is the interdisciplinary study of educational experience." For me, it includes the intersection of questions of knowledge, value, teacher preparation, education policy and resourcing, staffing, community economies, and the sustainability of rural communities. (p. 94)
Making connections between disconnected learning areas#
Boaler (2015) argues
Curriculum standards often work against connection making, as they present mathematics as a list of disconnected topics. But teachers can and should restore the connections by always talking about and valuing them and asking students to think about and discuss connections. (p. 184)
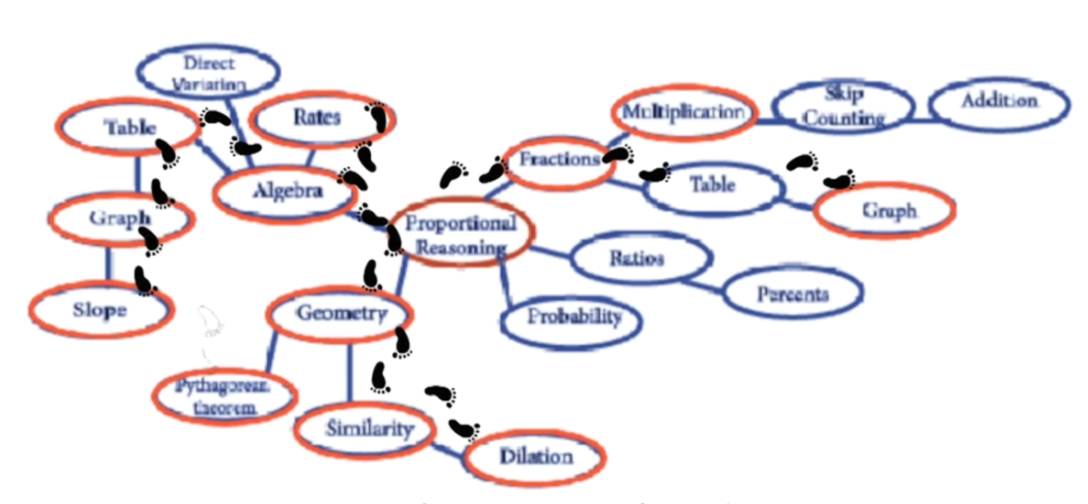
Boaler's YouCubed project provide a video "Tour of Math Connections to illustrate how topics of number, geometry, and algebra are connected under the big idea of proportional reasoning.
What interfaces might help enable this connection making? To enable the necessary gathering and weaving?
Boaler makes a similar point in this video in which she talks about work she's contributing to on a "Big Ideas" driven mathematical framework for California.
(adapted from YouCubed's Tour of Mathematical Connections)
Simeon (2021) emphasis added
One of the most damaging aspects of school mathematics, particularly as it is represented in commercial texts and computer-based mathematics programs is the atomisation of the curriculum into a seemingly endless list of discrete ‘topics’ where ‘coverage’ becomes the major goal of planning, the predominant mode of learning is ‘example/demonstrate-practice-practice’, and the majority of those exercises remain as they were observed by Vincent and Stacey in 2008 as relatively low-level, skill based repetitious exercises. (p. 8)
California's Mathematics Framework - Big Ideas#
Schwartz (2023) provides background on the development, nature, and reaction to California's new Math Framework. "Big ideas in mathematics" are outlined and intended to drive instruction which draws on inquiry-based instruction. It apparently is intended to "illustrate the connections across topics, both within the grade and between grades". Apparently, it is the inquiry-based part that has drawn the most flack.
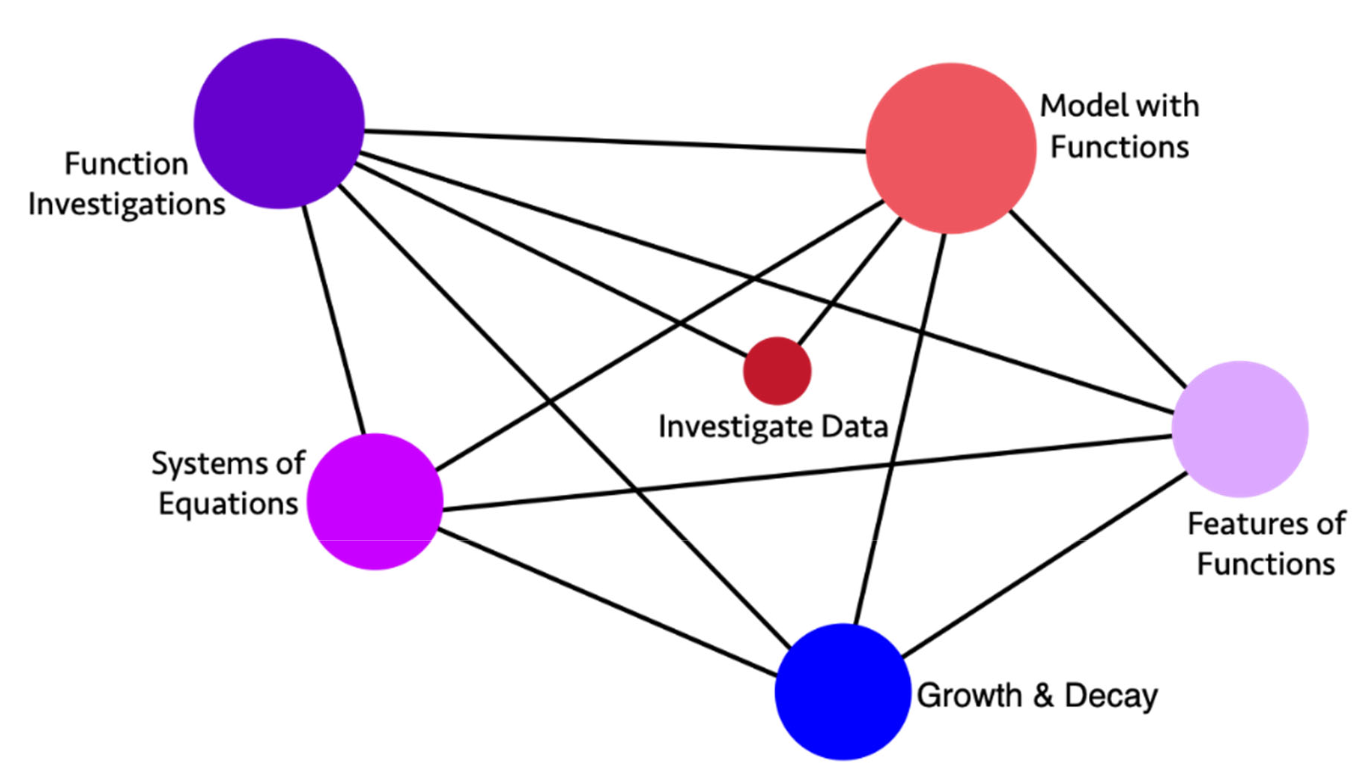
The framework documents specify the big ideas by year and represented with images like the following Big Ideas Map for Algebra 1. The size of the circles represent the importance of the ideas.
(adapted from Chapter 8 of California's 2023 Mathematics Framework, p. 38)
These images are supplemented with a table that provides more detail on the big ideas. Connecting each big idea with related content and then relevant content standards.
(adapted from Chapter 8 of California's 2023 Mathematics Framework, p. 39)
Rural students and making connections to cultural context#
Roberts, 2023a focuses on the challenge of closing the gap between city and country students. Arguing that incentives to lure students isn't enough. Instead, pointing to research (Dobrescu et al, 2021) that found modifications to the cultural context in NAPLAN tests reduced gaps by 33% (rural-urban) and 50% (Indigenous students). However, recent reforms make it more difficult to make these changes
Before the Gonski reforms, Australia had specific programs that helped teachers make their teaching material more relevant to rural students. These were removed for a more explicit one-size-fits-all model. We know that students learn by first connecting new concepts to their experience, but under the current model the opportunity to do this is actively removed. When teachers’ work is reduced to dishing out pre-prescribed materials and focused on narrow measures, it is no wonder that we have a staffing shortage. We are actively de-professionalising the very people we need to turn things around
Increasing cash bonuses, rental subsidies and transfer rights to teachers cannot overcome the persistent undermining of their professional work. Indeed, the most common sentiment I hear from rural teachers is that they are too busy to teach, to make the curriculum meaningful for their students and to build the very relationships that motivated them to enter the classroom in the first place.
The education system likes to ignore that rural Australia exists as a distinct space with distinct cultures, knowledges and histories. Instead, its focus on standardisation ensures rural students struggle to see themselves or their communities in education. I’m yet to meet a parent whose aspirations for their child’s education is a Naplan or HSC grade, but that is the focus of policymakers.
More formal discussion of these ideas in Roberts (2023b)
Making connections in general (mathematics)#
Boaler (2015) also offers a collection of norms/advice to help teach mathematics. In theory, something like this (or other pedagogical/other frameworks) could also be useful in terms of connections with/to/from the curriculum and its components.
Boaler (2015) writes
Teachers are usually given long lists of content to teach, with hundreds of content descriptions and no time to go into depth on any ideas. When teachers are given lists of content to teach, they see a subject that has been stripped down to its bare parts like a dismantled bike—a collection of nuts and bolts that students are meant to shine and polish all year. Lists of contents don't include connections; they present mathematics as though connections do not even exist. I don't want students polishing disconnected bike parts all day! I want them to get onto the assembled bikes and ride freely, experiencing the pleasure of math, the joy of making connections, the euphoria of real mathematical thinking
Question being how to enable ad hoc connection maps between the different components in the curriculum? For separate purposes.
Perhaps the very essence of gather/weave.
Li et al (2019) identify three types of knowledge components that make up mathematics conceptual knowledge for teaching. The second - being able to connect and justify the main points of a content topic, and to place it in wider contexts - is directly challenged by requiring conceptual knowledge that across different connected topics. - even suggesting it is the one with which students have the least familiarity.
Promoting conceptual understanding#
Richland et al (2012) cite a meta-analysis by Hiebert and Grouws (2007) and findings that two broad features of instruction promote students' understanding of the conceptual structure of mathematics. Findings corroborated in the TIMSS video studies
-
"treating mathematically connections in an explicit and public way"
discussing the mathematical meaning underlying procedures, asking questions about how different solution strategies are similar to and different from each other, considering the ways in which mathematical problems build on each other or are special (or general) cases of each other, attending to the relationships among mathematical ideas, and reminding students about the main point of the lesson and how this point fits within the current sequence of lessons and ideas. (p. 384)
-
struggle - "students expend effort to make sense of mathematics, to figure out something that is not immediately apparent" (p. 387)
The TIMSS video studies found that
It was neither the kinds of problems presented nor teaching style employed that differentiated the high-achieving countries from the others, but the kinds of learning opportunities teachers created for students, namely, making explicit connections in the lesson among mathematics procedures, problems, and concepts and finding ways to engage students in the kind of productive struggle that is required to understand these connections in a deep way. (Richland et al 2012)
Richland et al (2012)
- identify a research agenda for solutions to the problem of teaching the conceptual structure of mathematics. One of which is for research into PD strategies that explore "how to impact teacher routines, particularly in the area of supporting students' connected, transferable thinking" (p. 199) because it has "proven difficult" to do.
- also report on research by Ma (1999) that found "U.S. teachers tended to represent the mathematics curriculum as linearly organized, whereas the Chinese teachers’ representations of the curriculum more closely resembled a web of connections" (p. 200) and suggest that greater understanding of teachers' knowledge of mathematics may aid in developing appropriate teaching practices etc.
Connections within mathematical tasks#
The maths-in-schools course provides the following example of the inter-connectedness of mathematical tasks
there are natural connections between them, and it is important to acknowledge the interconnectedness of the content in many aspects of maths learning in a classroom. For example, determining the area of a circle draws on students’ knowledge and understanding of the dimensions of a circle (Space), the use of a formula (Algebra) and knowledge of rounding decimals (Number) and the use of square units (Measurement) to communicate a solution.
Mismatch between rich mathematical tasks and the curriculum#
Liljedahl (2020) identifies a problem that is common to rich and engaging mathematical tasks as
they are, for the most part, all non-curricular tasks. That is, very few of these tasks require mathematics that map nicely onto a list of outcomes or standards in a specific school curriculum. (p. 24)
He goes onto describe how the "open-middle" in many mathematical tasks (see low-floor-high-ceiling-wide-walls#Low-floor, open-middle, high-ceiling tasks) can make this even more difficult. i.e. of the many different paths that may be used to solve a mathematical task, only one may be the "curricular" path. A path that no student may choose to walk.
The intent (or even need for) more alignment with the curriculum can lead to adding constraints to a task which can lead to reducing "what was once a rich task to the type of word problem we often see in mathematics textbooks" (p. 25)
Whereas rich tasks get students to think at the expense of meeting curriculum goals, word problems more predictably and reliably push students to use specific bits of learned knowledge - but often at the expense of engagement and the thinking that we need to foster in our students. (p. 25)
Clever approaches to curriculum visualisation?#
Michaela Epstien asks about "other clever approaches to curriculum visualisation". Sparked by hearing designers talk about the impact of even the smallest combinations of words and images on meaning she asks what curriculum design tells us. Her response?
The curriculum is linear.
She gives alternative004-exploring-oz-dev-logntly )
Yes, and also need to think about the affordances those designs provide (and to whom).
To do#
Boundary objects#
The idea of what we're forming here is a boundary object(s). Mediating between different professional communities, with different purposes. Echoes of the challenge facing gatherers-weavers-augmenters and epistemic-fluency
Robutti, O., Aldon, G., Cusi, A., Olsher, S., Panero, M., Cooper, J., Carante, P., & Prodromou, T. (2019). Boundary Objects in Mathematics Education and Their Role across Communities of Teachers and Researchers in Interaction. In International Handbook of Mathematics Teacher Education: Volume 3 (pp. 211--240). Brill. https://doi.org/10.1163/9789004419230_009
References#
Barker, P. (2020, August 19). Mapping learning resources to curricula in RDF --- Sharing and learning Phil Barker's work. Sharing and Learning. https://blogs.pjjk.net/phil/mapping-learning-resources-to-curricula-in-rdf/
Boaler, J. (2015). Mathematical Mindsets: Unleashing Students’ Potential Through Creative Math, Inspiring Messages and Innovative Teaching. John Wiley & Sons, Incorporated.
Dobrescu, L., Holden, R., Motta, A., Piccoli, A., Roberts, P., & Walker, S. (2021). Cultural Context in Standardized Tests (SSRN Scholarly Paper 3983663). https://doi.org/10.2139/ssrn.3983663
Eriksson, H. (2015). Digitizing Curricula: An Approach for Digital Usability. eChallenges e-2015 Conference, Vilnius, Lithuania. https://doi.org/10.1109/eCHALLENGES.2015.7441086
Golder, D., Kneebone, L., Phipps, J., Sunter, S., & Sutton, S. A. (2010). A configurable RDF editor for Australian curriculum. Proceedings of the Role of Digital Libraries in a Time of Global Change, and 12th International Conference on Asia-Pacific Digital Libraries, 189--197.
Li, Y., Pang, J., Zhang, H., & Song, N. (2019). Mathematics Conceptual Knowledge for Teaching: Helping Prospective Teachers Know Mathematics Well Enough for Teaching. In International Handbook of Mathematics Teacher Education: Volume 1 (pp. 77--104). Brill. https://doi.org/10.1163/9789004418875_004
Liljedahl, P. (2020). Building Thinking Classrooms in Mathematics, Grades K-12: 14 Teaching Practices for Enhancing Learning. Corwin Press.
On closing the divide between city and country students in Australia, we keep repeating past mistakes. (2023, September 10). The Guardian. https://www.theguardian.com/australia-news/2023/sep/11/on-closing-the-divide-between-city-and-country-students-in-australia-we-keep-repeating-past-mistakes
Richland, L. E., Stigler, J. W., & Holyoak, K. J. (2012). Teaching the Conceptual Structure of Mathematics. Educational Psychologist, 47(3), 189--203. https://doi.org/10.1080/00461520.2012.667065
Roberts, P. (2023a, September 10). On closing the divide between city and country students in Australia, we keep repeating past mistakes. The Guardian. https://www.theguardian.com/australia-news/2023/sep/11/on-closing-the-divide-between-city-and-country-students-in-australia-we-keep-repeating-past-mistakes
Roberts, P. (2023b). Contemplating curriculum in an urban world. Curriculum Perspectives, 43(1), 93--96. https://doi.org/10.1007/s41297-023-00194-y
Schwartz, S. (2023, July 13). California Adopts Controversial New Math Framework. Here's What's in It. Education Week. https://www.edweek.org/teaching-learning/california-adopts-controversial-new-math-framework-heres-whats-in-it/2023/07
Ward, N., & Nicholas, N. (n.d.). Benefits of Machine Readable Curricula. http://www.achievementstandards.org/sites/default/files/BenefitsMachineReadableCurricula_Mar10.pdf