CSER Maths in Schools - Practices and pedagogies
See also: maths-in-schools, teaching-mathematics
Examines several practices/pedagogies for exploring mathematical concepts and ideas. Uses the add to your toolkit metaphor.
Overview#
Starts with the disclaimer about the complexity of teaching. Multiple approaches chosen by teachers based on their assumptions of how to produce certain outcomes and the fit with the concept/skill and students.
References Hattie's Visible Learning work and offers the following image adapted from Hattie's work and the Victorian DoE's 10 high-impact strategy work.
Are there inconsistencies (and related issues) in the provided advice?
Given the complexity and entanglement of teaching and the standard atomisation involved in formal research etc (i.e. all-models-are-wrong) there is likely to be inconsistencies in the advice provided. Especially in a course like this which seeks to weave together multiple sources of advice. For example
-
Variety versus consistency/cognitive load.
The summary of the overview recommends using "a variety of pedagogies" to aid inclusion/engagement etc.
-
Ability grouping or not?
Boaler and other references from the first module in this course argues against ability grouping. But Hattie's visible learning identifies ability grouping for gifted students as a positive. The distinction ("for gifted students") perhaps points at some of the complexity here.
Targeted teaching#
The first of three "key considerations" included in the overview illustrates that complexity. targeted-teaching (a "variation" of assessment-for-learning) could be seen as a fine-grained version of ability grouping. On the plus side it is losing what perhaps creates the issues with ability grouping - encouraging a fixed mindset - but at the cost of sustainability as a teacher tries to cater for each student's needs.
Explicit advice is given that at the start of the year, test students to see what they recollect from the year before. Given the cumulative nature of the Australian Curriculum.
AC learning progression extracts
The numeracy capability provides a "comprehensive view of observable progressive indicators" of K&S in numeracy concepts. Suggested it is linked to the content descriptions in some areas.
Task for exploring-australian-curriculum
Manipulatives, modelling, and mathematical modelling#
Manipulatives positioned as both physical and digital. Linked to enactive-mathematics-pedagogy
Transference#
Ability to apply K&S in a different setting.
Some methods suggested to be picked up below
- UDL and CRA for showing multiple representations - showing multiple situations
- CRM to enable transfer to family/community.
- Opportunity to apply to unfamiliar situations.
- Establish clearly concept being learned.
- Raise awareness of inter-connections.
- Across year-level curriculum
- other curriculum
- Opportunity to learn beyond set classwork/simple tasks.
- Using patterns to build understanding.
- Growth mindset.
Also points to work on the nature of instructions and their impact on performance, learning, and transfer. But only examines it at the surface level.
Universal Design for Learning (UDL)#
Highlights the diversity in the student body and some ways the australian-curriculum etc support this.
Positions UDL as "one pedagogy that can support an inclusive maths classroom". UDL is a framework suggesting that learners (brains) are composed of three different networks:
- recognition;
- strategic;
- affective.
Aims to provide students with multiple means of
-
engagement - affective networks, the why of learning,
Choice in activities. Managing the flow and ZPD. Encouragement and feedback. SRL.
-
representation - recognition networks, the what of learning, and
Multiple representations/media. Defining terms. Dual-encoding. Connections. Templates and checklists.
-
action/expression - strategic networks, the _how" of learning.
Different demonstrations of learning. Concept maps.
The assumption being that rather than provide adaptations for different people, design universal approaches that reduce barriers for all.
Is a universal design possible and/or sustainable?
The example given is of an entrance to a build that is up a flight of stairs. An adaptation approach might provide a lift for those with other needs. A UDL approach would design a single solution for all. e.g. a ramp rather than a set of stairs.
There are challenges behind this assumption
- Is it a green field design?
i.e. the entrance may already be designed and built. It may not possible (sustainable) to replace the stairs with a ramp.
- Is a ramp universal?
My first thought examining the ramp is that my mother couldn't use it. It's too steep.
A need for greater digital CASA to support variety
The video closes with questions for planning asking "how can I provide multiple ways to engage learners/use different representations/to assess learners"
That variety of different approaches need to be gathered and woven into sustainable practice. Doing this manually will be a pain.
Engagement#
Focus here is flexibility in task design. Motivate students differently by using different tasks.
Example given is for right-angled triangles.
Representation#
Multiple media in presenting information.
Action & Expression#
Related to different tasks
Explicit teaching#
Explicit teaching practices show students clearly what to do and how to do it, and in doing so, they provide instruction, demonstrate concepts and build student knowledge and skills. In this process, students are not left to construct information themselves; rather, they are guided step-by-step using a systematic and sequential approach.
Sounds very much like a reactionary response to (extreme versions of) inquiry learning. The characteristics given at the end of that quote "step-by-step using a systematic and sequential approach" especially. Goes onto offer some additional specifications.
External consistency - productive-failure
Sounds like productive-failure would clash with some of the assumptions here. Similarly contemplate-then-calculate type activities. But again that may be a question of definitions.
Concrete, Representational (or Pictorial), Abstract (CRA)#
A framework that combines instructional methods to teach maths effectively. Video explanation starts off with the question
How can we teach students complex and abstract mathematical concepts?
Sequence or not?
There is a tendency to think of this as a sequential progression. The introduction and assessment does treat each of the phases as distinct and Bruner seemed to suggest that sequence helped learning.
Concrete and/or contextual?
Wondering if the concrete could sometimes be interpreted as contextual, especially in older learners in the midst of a lesson sequence.
i.e. if and what might be the relationship between a physical manipulative and a problem/tasks that is deeply contextual to the learner?
Math investigations#
Points to resolve-mathematics-by-inquiry
guided pedagogical approach that involves learning and applying maths through investigations and solving problems....tap into students' curiosity and allow new opportunities to transfer...can follow or be combined with explicit teaching
Interesting inclusion of guided""
Use of guided above suggests explicit opposition to discovery or inquiry approaches.
Investigations can be cyclical and iterative
-
Question
- Set by teacher
- students offering required sub-questions
-
Investigate
- What do students know?
- What do they need to know
- Explore how to answer
- may require some teaching
-
Apply & model
- done by students, carry out mathematical tasks
- record findings and process
-
Discuss & defend
- Use of maths language in context
- Make explicit mathematical thinking
-
Reflect
- Students consider futher questions
- Teacher ponders any required re-teaching
Culturally responsive maths pedagogy#
Establishes the diversity of Australian society. Celebrating that diversity is important. "CRM" pedagogy is a way to harness that diversity to increase interest. An approach that contextualises maths in the students' lives, communities, and culture.
Beyond this the video introduction shows the "CRM" pedagogy resonates other approaches (e.g. mathematical-mindsets, effective-pedagogy-in-mathematics), including
- have high expectations for all students;
- nurture quality, respectual, caring relationships
- see diversity and students' funds of knowledge as an asset
- connect learning to students' life-worlds
- involve students in meaningful projects
Goompi model#
See goompi-model
8Ways of learning#
Designed to meet needs on Aboriginal students (NSW DoE) and engage all learners. 8 principles/ways of learning to engage with local communities
- Story sharing - use narrative to approach learning - we connect through the stories we share
- Learning maps - explicitly mapping/visualising processes because we picture our pathways of knowledge
- Non-verbal - applying intra-personal and kinaesthetic skills to thinking/learning - we see, think, act, make and share without words
- Symbols & images - using images/metaphors to understand concepts/content because we keep and share knowledge with art and objects
- Land links - place-based learning, linking content to local land and place because we work with lesson from land and nature
- Non-Linear - producing innovations & understanding by thinking laterally or combining systems because we put different ideas together and create new knowledge
- Deconstruct Reconstruct - modelling and scafollding, working from wholes to parts (watch then do) because we work from wholes to parts, watching and then doing
- Community links - centring local viewpoints, applying learning for community benefit because we bring new knowledge home to help our mob
Integrating the Goompi Model and elements of 8Ways#
Suggests that the Goompi model can be connected to each of the 8 ways. Illustrates this with four examples.
Material culture.#
Links to traditional basket weaving linked to surface area/volume calculations. Lessons start using the RAMR model
- Reality - sharing stories, videos etc.
- Abstraction - has students drawing/representing objects
- Maths - cover mathematical topics
- Reflection - students design artefacts for a specific purpose, critiquing the how/why of their designs
Data sovereignty (Yrs 7-8)#
Links to moves by indigenous communities to take control of their data. Students use data from the Reconciliation Barometer website to interpret and analyse data.
- Reality - introduce reconciliation and engage in discussion
- Abstraction - Introduce the barometer website and students start looking for answers
- Maths (DeConstruct/Reconstruct) - explanations and student investigations
- Reflection - students report findings and discuss what has been revealed
Data sovereignty (Yrs 9-10)#
Explore bias etc in government data about indigenous people (e.g. Closing the Gap)
- Reality (story telling) - explore/discuss the Closing the Gap report.
- (Learning maps) - discuss the next steps in learning and invite input
- Abstraction (Symbols and images) - view the report, interpret data and representations, students record questions, challenges
- (Land Links) - Ponder the geography of the data
- (Non-linear) - what connections can be made to other curricula, issues, etc
- Maths (DeConstruct/Reconstruct) - discuss sampling techniques etc.
- Critical REflection (Community links) - What data is included, what's not etc.
Whole school approach (8Ways)#
Draws on work from a "Closing the Gap" project - Make it count. Including work from Tyson Yunkaporta who apparently was involved in the development of the 8Ways.
Work that led to an approach called 8 + 1 ways. That added modelling assessment items/tasks, provision of key ideas, success indicators at the beginning of a learning sequence.
Module task: Practice and pedagogies#
- Need to integrate ideas/content from cser-content-in-action-connection-with-community module
Three options
-
Classroom activity ✔
Take on practice/pedagogy and create/adapt an existing classroom activity
- identify the approaches used
- describe the mathematics covered in the activity
- explain what you would do in the activity, including relevant resources
- provide tips for other teachers that can guide their use of the approach
- Use the hashtag #LessonPractices
-
Family information session
- Teacher workshop
The working title - which I may not tell students - for this learning activity is "What is mathematics? Why should I care?". It's intended to be a key part of any first lesson in a mathematics class. The aims being to
- Engage students' conceptions of what mathematics is/isn't and hopefully start developing a more positive outlook.
- Establish some routines (discussion, collaborative work, reflection etc.) that will be used in the class.
- Have a very low floor in terms of required mathematical knowledge.
The approaches used#
Early thinking has been on-going for a while but the this module has provided some very useful explicit connections with the the Goompi model, the related RAMR framework from Yumi Deadly Maths, and the 8Ways of learning. But there are also connections with mathematical investigations and CRA (e.g. YDM is explicitly influenced by Bruner)
Mathematics to be covered#
The key mathematics covered this activity is around the question "What is mathematics? Why should I care?". Rather than explicitly linked with specific content descriptions the intent is to help students start to appreciate the value, aesthetic, and purpose of mathematics.
With the intent to have a low floor and be applicable at most year levels the activity will introduce the concept of magic squares. Students will be expected to draw on some existing mathematical knowledge ranging from addition to perhaps some algebra.
Tips#
Limited practical tips since the activity is still in the planning phase. However, the current design is tightly connected to the purpose of setting up an on-going set of routines and expectations for a class. If those routines/expectations don't fit your class, some modification of the design would be advisable.
What will we do#
Reality#
Engage in discussions about
- What is mathematics
- How it is/isn't relevant to students and people in general.
- What would make it relevant?
Organise students into small groups, introduce the card game Number Scrabble (aka 15), play a game with them, before they play a few rounds.
Challenge the students to start thinking about winning strategies for Number Scrabble.
Abstraction#
Before the students start playing themselves. Provide them with a template to track the steps and outcomes of games. The numbers each player draws, if they won etc.
After a few rounds ask for any winners to share their strategies.
(Non-linear) engage in discussion about the strategies they've come up with. Ask/help them to make explicit connections to mathematics they've learned so far. Talk about how well those methods worked.
Depending on time, get the students to play another few rounds to put these strategies into practice. Discuss if/how overall performance changed.
Mathematics#
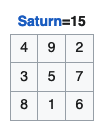
Introduce magic squares including giving its history of usage across cultures (e.g. China, Japan, India etc.). Ending with the planetary squares from Europe (around 1531) and see if anyone makes a connection between Saturn's square and Number Scrabble.
Ask the students to play a few more games of Number Scrabble. See if they've come up with any new strategies 😊.
Introduce the Goompi model and talk more about the view of mathematics it encompasses.
Reflection#
Engage in a discussion about the implications of this view for the question of "what is mathematics and why is it important (to me)?".
Link this to on-going practices and expectations for the class. Ask the students to start thinking about what parts of reality they'd like to explore in the future and explain how we'll try to support that exploration.